Hello friends again! I'm currently working on a Face Recognition project, using average half faces. I'm using the eigenface technique for face recognition. Since I'm a novice myself in this area, I did an extensive search on the net for understanding the bare concepts of this technique. So here I'm posting all the knowledge I gathered. I hope it helps you in thinking in the right direction if you are confused.
Please note that I have collected this information from many sources, so at the end of my post I'm providing the references. Heartfelt thanks to all of them. And by mistake, if I published someone's work here and did not mention his/her name, kindly inform me through mail, along with a link to your work, and I will be glad to correct my mistake.
So here we go!
Notice that there is an additional “eye localizer” in this system. Due to all kinds of the variations that may occur in the image (as discussed below), the face detector usually produces only an “approximate” location of the face. In order to find the “exact” location of the face for recognition, face recognition system designers often use the locations of both eyes for assistance. In this system, all the three functional modules (face detector, eye localizer, and face recognizer) follow the “feature extractor + pattern recognizer” schematics.
In the above figure, a face that was in the training database was reconstructed by taking a weighted summation of all the basis faces (eigen faces) and then adding to them the mean face.
In this figure there are two sets of data, one belonging to class A and the other belonging to class B. We have to draw a vector in a direction along which the distance between these two classes of data is maximized. The directions of the first two vectors are not efficient because they are unable to clearly distinguish between the two sets of data (as can be seen by the projection of the points on the vectors). However, the third and fourth vectors (especially the third one) are able to clearly separate the data sets. Hence, we choose the third and fourth eigenvectors (or principal components) as they represent the direction of greatest variation in the data.
The eigen vector is in the direction of maximum variation in these images.
In the above figure, there are six eigenvectors w1, w2, . . . , w6 (but we have shown only three), and an image is represented in the Eigenspace as a weighted combination of these eigenvectors (or eigenfaces). These eigenvectors act like axes in the Eigenspace. Just like a point in a 3D system (having x, y and z axis) is represented as (x,y,z), in the same way, an image in eigen space is represented as (w1, w2, . . . , wn), where w1, w2, . . . , wn are the eigenvectors and act as the axes of the eigen space.
Consider a simplified representation of the face space as shown in the figure above. The images of a face, and in particular the faces in the training set should lie near the face space, which in general describes images that are face like.
Please note that I have collected this information from many sources, so at the end of my post I'm providing the references. Heartfelt thanks to all of them. And by mistake, if I published someone's work here and did not mention his/her name, kindly inform me through mail, along with a link to your work, and I will be glad to correct my mistake.
Also, at some places I have pasted images of some symbols instead of inserting them, (like using instead of writing Φi ) because I haven't yet got the hang of font and formatting in this blog. So forgive me for that.
instead of writing Φi ) because I haven't yet got the hang of font and formatting in this blog. So forgive me for that.
 instead of writing Φi ) because I haven't yet got the hang of font and formatting in this blog. So forgive me for that.
instead of writing Φi ) because I haven't yet got the hang of font and formatting in this blog. So forgive me for that. Face Recognition using Eigenfaces, with an introduction to using the Average Half Face
Introduction
In today's
networked world, the need to maintain the security of information or physical
property is becoming both increasingly important and increasingly difficult.
From time to time we hear about the crimes of credit card fraud, computer
break-ins by hackers, or security breaches in a company or government building.
In most of these crimes, the criminals were taking advantage of a fundamental
flaw in the conventional access control systems: the systems do not grant
access by "who we are", but by "what we have", such as ID
cards, keys, passwords, PIN numbers, or mother's maiden name. None of these
means are really define us. Rather, they merely are means to authenticate us.
It goes without saying that if someone steals, duplicates, or acquires these identity
means, he or she will be able to access our data or our personal property any
time they want. Recently, technology became available to allow verification of
"true" individual identity. This technology is based in a field
called "biometrics". Biometric access control are automated methods
of verifying or recognizing the identity of a living person on the basis of
some physiological characteristics, such as fingerprints or facial features, or
some aspects of the person's behavior, like his/her handwriting style or
keystroke patterns. Since biometric systems identify a person by biological
characteristics, they are difficult to forge.
Face recognition is one of the few biometric methods that
possess the merits of both high accuracy and low intrusiveness. It has the
accuracy of a physiological approach without being intrusive. For this reason,
since the early 70's, face recognition has drawn the attention of researchers
in fields from security, psychology, and image processing, to computer vision.
While network security and access control are it most widely discussed
applications, face recognition has also proven useful in other
multimedia information processing areas. It could also be used to
obtain quick access to medical, criminal, or any type of records. Solving this
problem is important because it could allow personnel to take preventive
action, provide better service - in the case of a doctor’s appointment, or
allow a person access to a secure area.
Many face recognition algorithms
have been developed and each has its strengths. Each share a common element
which is that they all input a full face image into the algorithm. However,
none of the methods currently exploit the inherent symmetry of the face for
recognition. In this paper we demonstrate the effectiveness of using the
average-half-face as an input to face recognition algorithms for an increase in
accuracy and potential decrease in storage and computation time. The average
half-face is a transformation method that attempts to preserve the bilateral symmetry
that is present in the face. We will implement this technique using an approach
called Eigenfaces. Eigenfaces, based on principal components analysis (PCA), is
arguably the best known face recognition method and is used extensively as a
benchmark for other methods.
Facial
recognition was the source of motivation behind the creation of eigenfaces. For
this use, eigenfaces have advantages over other techniques available, such as
the system's speed and efficiency. Using eigenfaces is very fast, and able to
functionally operate on lots of faces in very little time. Unfortunately, this
type of facial recognition does have a drawback to consider: trouble
recognizing faces when they are viewed with different levels of light or
angles. For the system to work well, the faces need to be seen from a frontal
view under similar lighting. Face recognition using eigenfaces has been shown
to be quite accurate. By experimenting with the system to test it under
variations of certain conditions, the following correct recognitions were
found: an average of 96% with light variation, 85% with orientation variation,
and 64% with size variation.
Generic
Framework
In most cases, a
face recognition algorithm can be divided into the following functional
modules: a face image detector finds the locations of human faces from a
normal picture against simple or complex background, and a face recognizer determines
who this person is. Both the face detector and the face recognizer follow the
same framework; they both have a feature extractor that transforms the
pixels of the facial image into a useful vector representation, and a pattern
recognizer that searches the database to find the best match to the
incoming face image. The difference between the two is the following; in the face
detection scenario, the pattern recognizer categorizes he incoming feature
vector to one of the two image classes: “face” images and “non-face images. In
the face recognition scenario, on the other hand, the recognizer classifies the
feature vector (assuming it is from a “face” image) as “Smith’s face”, “Jane’s
face”, or some other person’s face that is already registered in the database.
The figure below depicts one example of the face recognition system.
Notice that there is an additional “eye localizer” in this system. Due to all kinds of the variations that may occur in the image (as discussed below), the face detector usually produces only an “approximate” location of the face. In order to find the “exact” location of the face for recognition, face recognition system designers often use the locations of both eyes for assistance. In this system, all the three functional modules (face detector, eye localizer, and face recognizer) follow the “feature extractor + pattern recognizer” schematics.
An Overview of the Eigenface method
Our aim is to
represent a face as a linear combination of a set of eigen images. This set of eigenfaces (or eigenvectors) can be generated by
performing a mathematical process called principal component analysis (PCA) on a large set of training images depicting different
human faces. Thereafter, any human face can be
considered to be a combination of this set of eigen faces. For example, one's face might be
composed of the average face plus 10% from eigenface 1, 55% from eigenface 2,
and even -3% from eigenface 3.
Mathematically:
where
represents the
face with the
mean subtracted from it,
represent weights and
the
eigenvectors.
The big idea is
that you want to find a set of images (called Eigenfaces, which are nothing but
Eigenvectors of the training data) that if you weigh and add together should
give you back an image that you are interested in. The way you weight these
basis images (i.e. the weight vector) could be used as a sort of a code for
that image-of-interest and could be used as features for recognition. Remarkably, it does not take many eigenfaces combined
together to achieve a fair approximation of most faces.
This can be
represented aptly in a figure as:
In the above figure, a face that was in the training database was reconstructed by taking a weighted summation of all the basis faces (eigen faces) and then adding to them the mean face.
First of all the idea of Eigenfaces considers face recognition as a 2-D recognition problem; this is
based on the assumption that at the time of recognition, faces will be mostly upright and frontal.
Because of this, detailed 3-D information about the face is not needed. This
reduces complexity by a significant bit.
Before the method for face recognition using Eigenfaces was introduced,
most of the face recognition literature dealt with local and intuitive
features, such as distance between eyes, ears and similar other features. This
wasn’t very effective. Eigenfaces inspired by a method used in an earlier paper
was a significant departure from the idea of using only intuitive features. It
uses an Information Theory approach wherein the most relevant face information is
encoded in a group of faces that will best distinguish the faces. It transforms
the face images in to a set of basis faces, which essentially are the principal
components of the face images.
The Principal Components (or Eigenvectors) basically seek directions in which
it is more efficient to represent the data. This is particularly useful
for reducing the computational effort. To understand this, suppose we get
60 such directions, out of these about 40 might be insignificant and only 20
might represent the variation in data significantly, so for calculations it
would work quite well to only use the 20 and leave out the rest. This is
illustrated by this figure:
In this figure there are two sets of data, one belonging to class A and the other belonging to class B. We have to draw a vector in a direction along which the distance between these two classes of data is maximized. The directions of the first two vectors are not efficient because they are unable to clearly distinguish between the two sets of data (as can be seen by the projection of the points on the vectors). However, the third and fourth vectors (especially the third one) are able to clearly separate the data sets. Hence, we choose the third and fourth eigenvectors (or principal components) as they represent the direction of greatest variation in the data.
In face recognition, we may think of classes A and B to be the training faces
of person A and person B. An eigenvector that can distinguish between these two
data sets would be more desirable in face recognition than an eigenvector that
cannot distinguish them. This is because if the vector is able to clearly
distinguish between the two sets of faces, the accuracy of face recognition
will be higher.
In some cases, the database will have only one or two images per person,
in which case the set of training images will not appear as distinct clouds,
but rather as a single cloud of random data points. In this case also, the
eigenvectors (or principal components) must be projected in the directions of
maximum data variation. Below are given two such eigenvectors:
We can imagine such a cloud of images as shown below:
The eigen vector is in the direction of maximum variation in these images.
When
we find the principal components or the Eigenvectors of the image set, each Eigenvector
has some contribution from EACH face used in the training set. So the
Eigenvectors also have a face like appearance. These look ghost like and are
ghost images or Eigenfaces. Every image in the training set can be represented
as a weighted linear combination of these basis faces.
In the above figure, there are six eigenvectors w1, w2, . . . , w6 (but we have shown only three), and an image is represented in the Eigenspace as a weighted combination of these eigenvectors (or eigenfaces). These eigenvectors act like axes in the Eigenspace. Just like a point in a 3D system (having x, y and z axis) is represented as (x,y,z), in the same way, an image in eigen space is represented as (w1, w2, . . . , wn), where w1, w2, . . . , wn are the eigenvectors and act as the axes of the eigen space.
The number of
Eigenfaces that we would obtain by performing PCA on the training image set
would be equal to the number of images in the training set. Let us take this
number to be M
. Like we mentioned before, some of these Eigenfaces (having
large eigen values) are more important in encoding the variation in face
images, thus we could also approximate faces using only the K
most
significant Eigenfaces.
Assumptions:
1. There are M images in the
training set.
2. There are K
most
significant Eigenfaces using which we can satisfactorily approximate a face.
Needless to say, K < M.
3. All images are N x N
matrices, which
can be represented as N2 x 1 dimensional vectors. This is done by concatenating all the N rows of a matrix into a single row,
which gives us a vector (a 1D array) of size N2. The same logic would apply to images that are not of
equal length and breadths. To take an example: An image of size 112 x 112 can
be represented as a vector of dimension 12544 or simply as a point in a 12544
dimensional space.
Note: The face images need not be square matrices. We have
considered images of dimension N x N, we could easily consider images of dimension m x N.
If you consider images of dimensions m x N then the vector would be of dimension
would be of dimension N m x 1. The matrix A would
then be of dimension mN x M, however AAT or the
covariance matrix C
would always be
a square matrix, irrespective of whether you choose square images or not.
 would be of dimension
would be of dimension
The matrix C would have to
be a square matrix as we are interested in finding the eigenvectors, and
eigenvectors are defined only for square matrices. I hope I could clear your
doubt.
Algorithm for Finding
Eigenfaces:
1. Obtain M training images I1, I2,
… IM , it is very important that the images are centered.
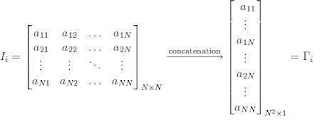
2. Represent each image Ii as a vector as discussed above. This is done by concatenating all
the rows of a matrix to form a vector, as shown below:
as discussed above. This is done by concatenating all
the rows of a matrix to form a vector, as shown below:
 as discussed above. This is done by concatenating all
the rows of a matrix to form a vector, as shown below:
as discussed above. This is done by concatenating all
the rows of a matrix to form a vector, as shown below:
For illustration purposes, we can imagine the above operation to be taking place somewhat as shown below:
Average face (or mean face) obtained by finding
the average of all the face vectors in the data set
4. Subtract the mean face from each face vector to get a set of
vectors
to get a set of
vectors
. The purpose of subtracting the mean image from each image
vector is to be left with only the distinguishing features from each face and
“removing”, in a way, information that is common.
 to get a set of
vectors
to get a set of
vectors
5. Find the Covariance matrix C
:
Note that the Covariance matrix has simply been made by
putting one modified image vector Φi
in one column each. Also note that C A is a N2 x M matrix.
6. We now need to calculate the Eigenvectors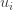 of C
of C
. However note that C
is a N2 x N2 matrix and it
would return N2 Eigenvectors
each being N2dimensional. For an image this number is HUGE. The
computations required would easily make your system run out of memory. How do
we get around this problem?
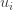 of C
of C
7. Instead of the Matrix AAT consider the
matrix ATA. Remember A
is a N2 x M matrix, thus ATA is a M x M
matrix. If we
find the Eigenvectors of this matrix, it would return M
Eigenvectors,
each of dimension M x 1, let’s call these Eigenvectors .
.
 .
.
Now from some properties of matrices, it follows that: . We have found out
. We have found out earlier. This
implies that using
earlier. This
implies that using we can
calculate the M largest Eigenvectors of AAT. Remember that M << N2
we can
calculate the M largest Eigenvectors of AAT. Remember that M << N2 as M is simply
the number of training images.
 . We have found out
. We have found out earlier. This
implies that using
earlier. This
implies that using we can
calculate the M largest Eigenvectors of AAT. Remember that M << N2
we can
calculate the M largest Eigenvectors of AAT. Remember that M << N2
8. Find the best M Eigenvectors of C = AAT by using the
relation discussed above. That is: . Also keep in mind that
. Also keep in mind that .
.
 . Also keep in mind that
. Also keep in mind that .
.
The M eigenvectors for the above set of M images will look something like as shown below:
9. Select the best K
Eigenvectors,
the selection of these
Eigenvectors is done heuristically.
[Best 6 Eigenfaces, assuming K=6]
Finding Weights:
The Eigenvectors found at the end
of the previous section,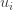 when converted
to a matrix in a process that is reverse to that in STEP 2, have a face like
appearance. Since these are Eigenvectors and have a face
like appearance, they are called Eigenfaces. Sometimes, they are also called as Ghost Images because of their weird
appearance.
when converted
to a matrix in a process that is reverse to that in STEP 2, have a face like
appearance. Since these are Eigenvectors and have a face
like appearance, they are called Eigenfaces. Sometimes, they are also called as Ghost Images because of their weird
appearance.
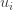 when converted
to a matrix in a process that is reverse to that in STEP 2, have a face like
appearance. Since these are Eigenvectors and have a face
like appearance, they are called Eigenfaces. Sometimes, they are also called as Ghost Images because of their weird
appearance.
when converted
to a matrix in a process that is reverse to that in STEP 2, have a face like
appearance. Since these are Eigenvectors and have a face
like appearance, they are called Eigenfaces. Sometimes, they are also called as Ghost Images because of their weird
appearance.
Now each face in the training set (minus the mean), Φi can be
represented as a linear combination of these Eigenvectors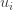
:
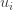
Each normalized training image is represented in this
basis as a vector.
where i = 1,2… M. This means we have to calculate such a
vector corresponding to every image in the training set and store them as
templates.
Recognition Task:
Now consider we have found out the Eigenfaces for the
training images, their associated weights after selecting a set of most
relevant Eigenfaces and have stored these vectors corresponding to each
training image.
Given an unknown face image to recognize,
- Compute a "distance"
between the new face and each of the training faces
- Select the training image
that's closest to the new one as the most likely known person
- If the distance to that face
image is above a threshold, "recognize" the image as that
person, otherwise, classify the face as an "unknown" person
Deciding on the
Threshold:
Why is the threshold important?
Consider for simplicity we have ONLY 5 images in the
training set. And a probe that is not in the training set comes up for the
recognition task. The score for each of the 5 images will be found out with the
incoming probe. And even if an image of the probe is not in the database, it
will still say the probe is recognized as the training image with which its
score is the lowest. Clearly this is an anomaly that we need to look at. It is
for this purpose that we decide the threshold. The threshold
is decided
heuristically.
Now to illustrate what we just
said, consider a simpson image as a non-face image, this image will be scored
with each of the training images. Let’s say
is the lowest
score out of all. But the probe image is clearly not belonging to the database.
To choose the threshold we choose a large set of random images (both face and
non-face), we then calculate the scores for images of people in the database
and also for this random set and set the threshold
accordingly.
More on the Face Space:
Here is a brief discussion on the face space.
Consider a simplified representation of the face space as shown in the figure above. The images of a face, and in particular the faces in the training set should lie near the face space, which in general describes images that are face like.
The projection distance
should be under
a threshold
as already
seen. The images of known individual fall near some face class in the face
space.
There are four possible combinations on where an input
image can lie:
1. Near a face class and near the face space: This is the
case when the probe is nothing but the facial image of a known individual
(known = image of this person is already in the database).
2. Near face space but away from face class: This is the
case when the probe image is of a person (i.e a facial image), but does not
belong to anybody in the database i.e. away from any face class.
3. Distant from face space and near face class: This
happens when the probe image is not of a face however it still resembles a
particular face class stored in the database.
4. Distant from both the face space and face class: When
the probe is not a face image i.e. is away from the face space and is nothing
like any face class stored.
Out of the four, type 3 is
responsible for most false positives. To avoid them, face detection is
recommended to be a part of such a system.
Average-Half-Face
Several previous
attempts to utilize the symmetry of the face for face recognition and face
detection have been made. It is well-known that the “face is roughly
symmetrical”. Zhao and Chellappa use the idea of face symmetry to solve the
problem of illumination in face recognition using Symmetric Shape-from-Shading,
while Ramanathan et al. introduce the notion of ‘Half-faces’ (in the sense of
exactly one half of the face) to assist in computing a similarity measure
between faces using images that have non-uniform illumination. In face
recognition, the use of the bilateral symmetry of the face has been limited to
extracting facial profiles for recognition.
The
average-half-face is inspired by the symmetry preserving singular value
decomposition (SPSVD). The SPSVD is used to reduce the dimensionality of data
while simultaneously preserving symmetry that is present in the data. Singular
Value Decomposition is a technique used in conjunction with Principal Component
Analysis (PCA) during extraction of Eigenvectors. When applied to face images,
this amounts to two steps. First, the image is centered about the nose of the
(properly oriented) face to represent the data as symmetric as possible. When
we speak of the data being symmetric, we mean that two spatial halves of the
data are similar, not that the matrix of the data itself is symmetric. Next,
the image is divided into two symmetric halves and they are averaged together
(reversing the columns of one of the halves first). Thereafter, we forward this
average-half face to the face recognition algorithm.
The figure above
displays the full face image, the left and right faces after centering, and the
average-half-face of an example image.
The average-half-face
can be seen as a preprocessing step to a face recognition algorithm. Feature
selection as well as subspace computation can be performed on the set of
average-half-faces just as is done on a set of full faces. Therefore, the
average-half-face can be applied to any face recognition algorithm that uses
full frontal faces as an input.
Algorithm
Outline:
1. Center and
orient the face in the image. This is done in our work by using the location of
the tip of the nose.
2. Partition the
image into two equal left and right halves, Il
and Ir.
3. Reverse of
the ordering of (or mirror) the columns of one of the images (in this case the
right image), producing Ir’.
4. Average the
resulting mirror right half image (Ir’)
with the left half image (Il)
to produce the average-half face.
The
average-half-face is then used in place of the full face image for face
recognition. The face recognition algorithm uses
eigenfaces to form two subspaces from the full face and average-half-face.
Then, the classification of test faces is done separately in these subspaces.
I hope this post
helped you. You are welcome to comment or ask questions. Au revoir!
References
·
Josh Harguess and J. K. Aggarwal. “A Case for the Average-Half-Face in 2D and 3D
for Face Recognition”
· "Eigenface."
Wikipedia, The Free Encyclopedia. http://en.
wikipedia.org/wiki/Eigenface
· “Eigenvector.” Wikipedia, The Free
Encyclopedia. http://en.wikipedia.org/wiki/Eigenvector
· “Facial Recognition System.” Wikipedia, The
Free Encyclopedia. http://en.wikipedia.org/wiki/Facial_recognition_system
· “Principal Component Analysis.” Wikipedia, The
Free Encyclopedia. http://en.wikipedia.org/wiki/Principal_component_analysis
· “Eigenface
Tutorial.” Drexel University. http://www.pages.drexel.edu/~sis26/Eigenface-Tutorial.htm
· Shubhendu
Trivedi. “Face Recognition using Eigenfaces and Distance Classifiers: A Tutorial”,
February 11, 2009. http://onionesquereality.wordpress.com/2009/02/11/
· Face-Recognition-using-Eigenfaces-and-Distance-Classifiers-A-Tutorial-Onionesque-Reality.htm/
· “Seeing With OpenCV, Part 4: Face Recognition With
Eigenface.” Cognotics http://www.cognotics.com/opencv/servo_2007_series/part_4/index.html
· Shang-Hung Lin. “An Introduction to Face Recognition
Technology”
· Jonathon
Shlens. “A Tutorial on Principal
Component Analysis.” Center for
Neural Science, New York University
· Tarun
Bhatia. “Principal Component Analysis (Dimensionality Reduction)”
· “Principal
Component Analysis.” Nonlinear Dynamics
Inc. http://www.nonlinear.com/products/progenesis/samespots/Principal-component-analysis/
· Andrew
Davison. “Face Recognition”. http://fivedots.coe.psu.ac.th/~ad/jg
· Josh
Harguess and J. K. Aggarwal. “Is There a
Connection Between Face Symmetry and
Face Recognition?”





















Great job!!
ReplyDelete